Flip Geodesics
This algorithm takes as input a path (or loop/network of paths) along the edges of a triangle mesh, and as output straightens that path to be a geodesic (i.e. a straight line, or equivalently a locally-shortest path along a surface). The procedure runs in milliseconds, is quite robust, comes with a strong guarantee that no new crossings will be created in the path, and as an added benefit also generates a triangulation on the surface which conforms to the geodesic. Additionally, it even enables the construction of Bézier curves on a surface.
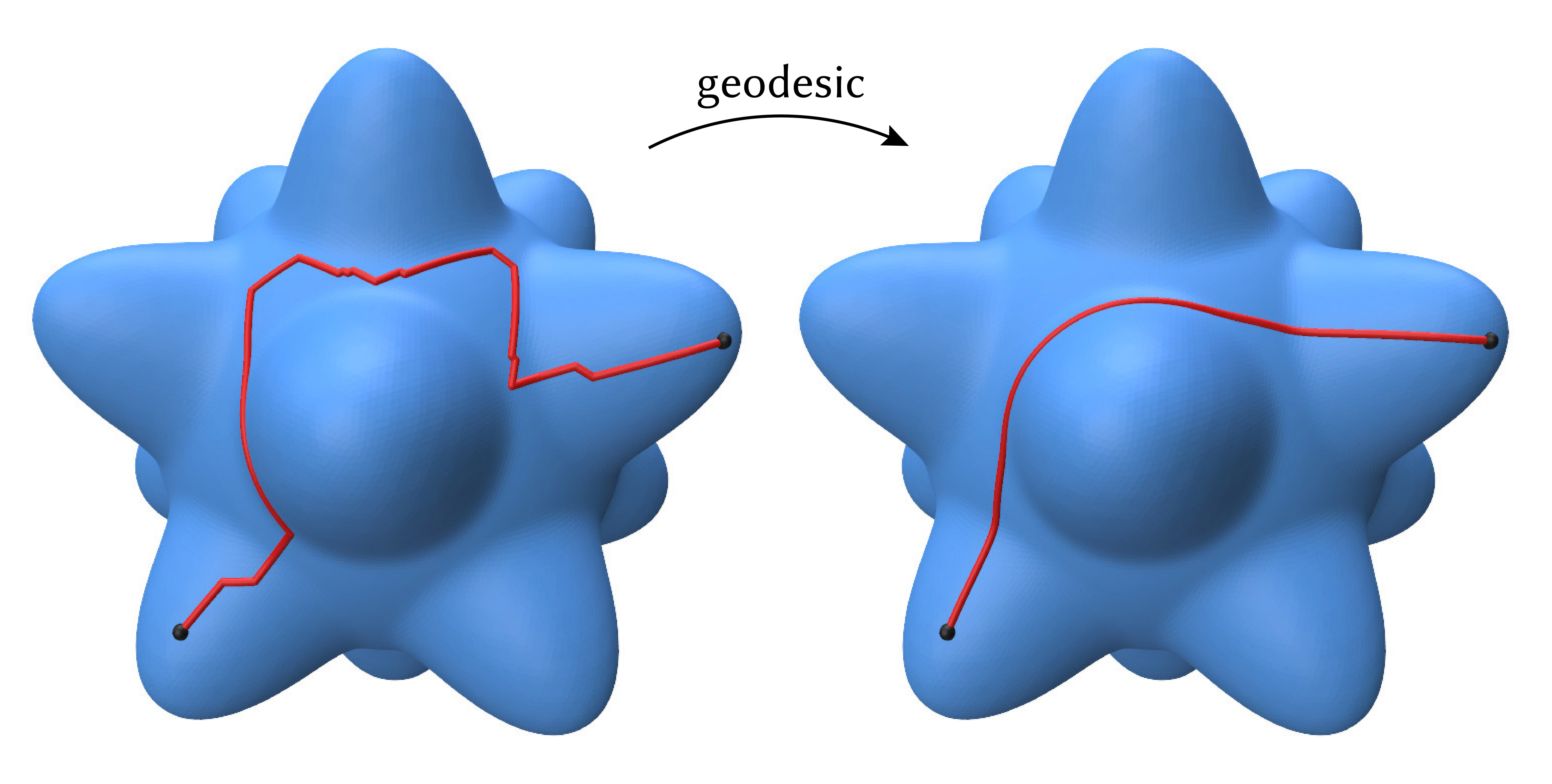
See this repo for a demo application which wraps this implementation as a standalone application with a GUI.
This is an implementation of the algorithm described in You Can Find Geodesic Paths in Triangle Meshes by Just Flipping Edges.
#include "geometrycentral/surface/flip_geodesics.h"
Example:
#include "geometrycentral/surface/flip_geodesics.h"
#include "geometrycentral/surface/meshio.h"
using namespace geometrycentral;
using namespace geometrycentral::surface;
// Load a mesh
std::unique_ptr<ManifoldSurfaceMesh> mesh;
std::unique_ptr<VertexPositionGeometry> geometry;
std::tie(mesh, geometry) = readManifoldSurfaceMesh("my_mesh.obj");
// Create a path network as a Dijkstra path between endpoints
std::unique_ptr<FlipEdgeNetwork> edgeNetwork;
Vertex vStart = mesh->vertex(0);
Vertex vEnd = mesh->vertex(7);
edgeNetwork = FlipEdgeNetwork::constructFromDijkstraPath(*mesh, *geometry, vStart, vEnd);
// Make the path a geodesic
edgeNetwork->iterativeShorten();
// Extract the result as a polyline along the surface
edgeNetwork->posGeom = geometry.get();
std::vector<std::vector<Vector3>> polyline = edgeNetwork->getPathPolyline3D();
Constructing a path network
The class stateful class FlipEdgeNetwork encapsulates all functionality in the algorithm; all of the methods below are members functions. This class wraps a SignpostIntrinsicTriangulation (as member FlipEdgeNetwork::tri), and also manages a path network along the edges of that triangulation.
The most direct construct takes as input a sequence of halfedges along the surface which comprise the path.
FlipEdgeNetwork::FlipEdgeNetwork(ManifoldSurfaceMesh& mesh, IntrinsicGeometryInterface& inputGeom, const std::vector<std::vector<Halfedge>>& paths, VertexData<bool> extraMarkedVerts = VertexData<bool>())
Construct a network of paths along the surface.
mesh: the input manifold triangle meshinputGeom: the input geometry (as always, aVertexPositionGeometryis valid input)paths: a collection of paths along the surface, each given as an ordered sequence of halfedgesextraMarkedVerts: if given, boolean vector of vertices where the path is pinned, and should not be straightened
Additionally, several factory methods are provided which assist in constructing a path network from common input data.
static std::unique_ptr<FlipEdgeNetwork> FlipEdgeNetwork::constructFromDijkstraPath(ManifoldSurfaceMesh& mesh, IntrinsicGeometryInterface& geom, Vertex startVert, Vertex endVert)
Construct a network consisting of a single path, generated by running Dijkstra’s algorithm between two point.
mesh: the input manifold triangle meshinputGeom: the input geometry (as always, aVertexPositionGeometryis valid input)startVert,endVert: the source and target vertices from which to initialize a Dijkstra path along edges
static std::unique_ptr<FlipEdgeNetwork> FlipEdgeNetwork::constructFromPiecewiseDijkstraPath(ManifoldSurfaceMesh& mesh, IntrinsicGeometryInterface& geom, std::vector<Vertex> points, bool closed = false, bool markInterior = false)
Construct a network consisting of a single path, generated by running Dijkstra’s algorithm between consecutive pairs of vertices.
mesh: the input manifold triangle meshinputGeom: the input geometry (as always, aVertexPositionGeometryis valid input)points: the not-necessarily-adjacent vertices from which to initialize the Dijkstra path, by running Dijkstra’s algorithm between each i’th and (i+1)’th points.closed: if true, the first point will be connected to the last to create a closed loopmarkInterior: if true, the path will be pinned at the specifiedpointsand not shortened there
static std::unique_ptr<FlipEdgeNetwork> FlipEdgeNetwork::constructFromEdgeSet(ManifoldSurfaceMesh& mesh, IntrinsicGeometryInterface& geom, const EdgeData<bool>& inPath, const VertexData<bool>& extraMarkedVertices)
Construct a network from a marked set of edges on the mesh. Endpoints, loops, etc are heuristically inferred (e.g. if a path ends at the same vertex it starts at, it is assumed to be a loop).
mesh: the input manifold triangle meshinputGeom: the input geometry (as always, aVertexPositionGeometryis valid input)inPath: a boolean array indicating edges which are in the pathextraMarkedVerts: if given, boolean vector of vertices where the path is pinned, and should not be straightened
FlipEdgeNetwork::reinitializePath(const std::vector<std::vector<Halfedge>>& paths)
Re-initialize an existing FlipEdgeNetwork object to hold the paths in paths, just like in the constructor. Useful when used in conjunction with rewind().
paths: a collection of paths along the surface, each given as an ordered sequence of halfedges
Manipulating paths
The key routine is FlipEdgeNetwork::iterativeShorten(), which shortens the path until it is a geodesic by flipping edges in the underlying intrinsic triangulation.
void FlipEdgeNetwork::iterativeShorten(size_t maxIterations = INVALID_IND, double maxRelativeLengthDecrease = 0.)
Shorten the network to be geodesic.
Additional termination conditions can be set to potentially stop the process before the path is a geodesic:
maxIterationsif set to something other thanINVALID_IND, limits the number of iterationsmaxRelativeLengthDecreaseif set to something other than0, limits the maximum decrease in length for the network. E.g.0.5would mean the resulting network is at at0.5 * L, whereLis the initial length.
Importantly, after calling iterativeShorten(), the underlying intrinsic triangulation FlipEdgeNetwork::tri is a triangulation which conforms to the generated geodesics. This triangulation can then be used for subsequent computation, such as solving a PDE which has geodesics as boundary conditions.
Shortening many paths
After shortening a path to a geodesic, the underlying triangulation has been mutated by edge flips. If you want to shorten another path, you can call rewind() to reset the data structure and prepare it for the next path.
For instance, if you wanted to find many point-to-point geodesic paths, you might write something like:
std::unique_ptr<FlipEdgeNetwork> flipNetwork(new FlipEdgeNetwork(*mesh, *geometry, {}));
flipNetwork->supportRewinding = true;
flipNetwork->posGeom = geometry.get();
for(/* each path to compute */) {
Vertex startVert; // populate these somehow
Vertex endVert;
// Get an initial dijkstra path
// (surface/mesh_graph_algorithms.h)
std::vector<Halfedge> dijkstraPath = shortestEdgePath(*geom, startVert, endVert);
// Reinitialize the ede network to contain this path
flipNetwork->reinitializePath({dijkstraPath});
// Straighten the path to geodesic
flipNetwork->iterativeShorten();
// Extract the path and store it in the vector
std::vector<Vector3> path3D = flipNetwork->getPathPolyline3D().front();
// Be kind, rewind
flipNetwork->rewind();
}
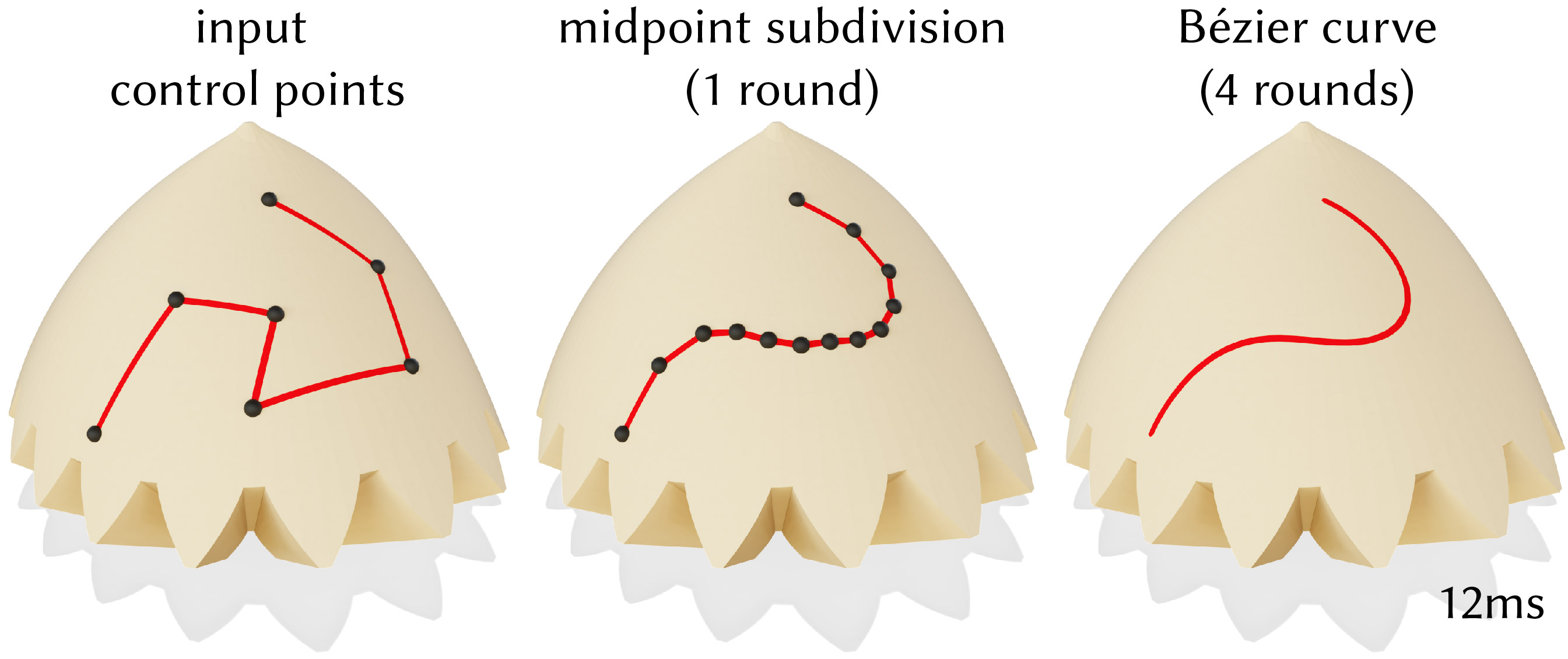
Geodesic Bézier curves
Once we can shorten curves to geodesics, we can use a de Casteljau-style subdivision scheme to construct geodesic Bézier curves along a mesh, using a procedure described in “Modeling on triangulations with geodesic curves” by Morera et al. (2008).
void FlipEdgeNetwork::bezierSubdivide(size_t nRounds)
Construct a Bézier curve from an input control polygon path via iterative subdivision.
nRoundsspecifies the number of subdivision rounds to perform; the curve converges to an exact geodesics asnRoundsincreases. SettingnRounds=3is often a good initial choice.
Note that the control points of the curve should be marked vertices, as described in the construction section. Additionally, this function should be applied to a network consisting of a single path, not distinct paths between multiple control points. Calling the factory method FlipEdgeNetwork::constructFromPiecewiseDijkstraPath(mesh, geom, /* vector of constrol vertices */, false, true) above will construct a path ready for Bézier subdivision.
The algorithm used here is essentially the one described in “Modeling on triangulations with geodesic curves” by Morera et al. (2008), but using flip-based geodesics to straighten paths.
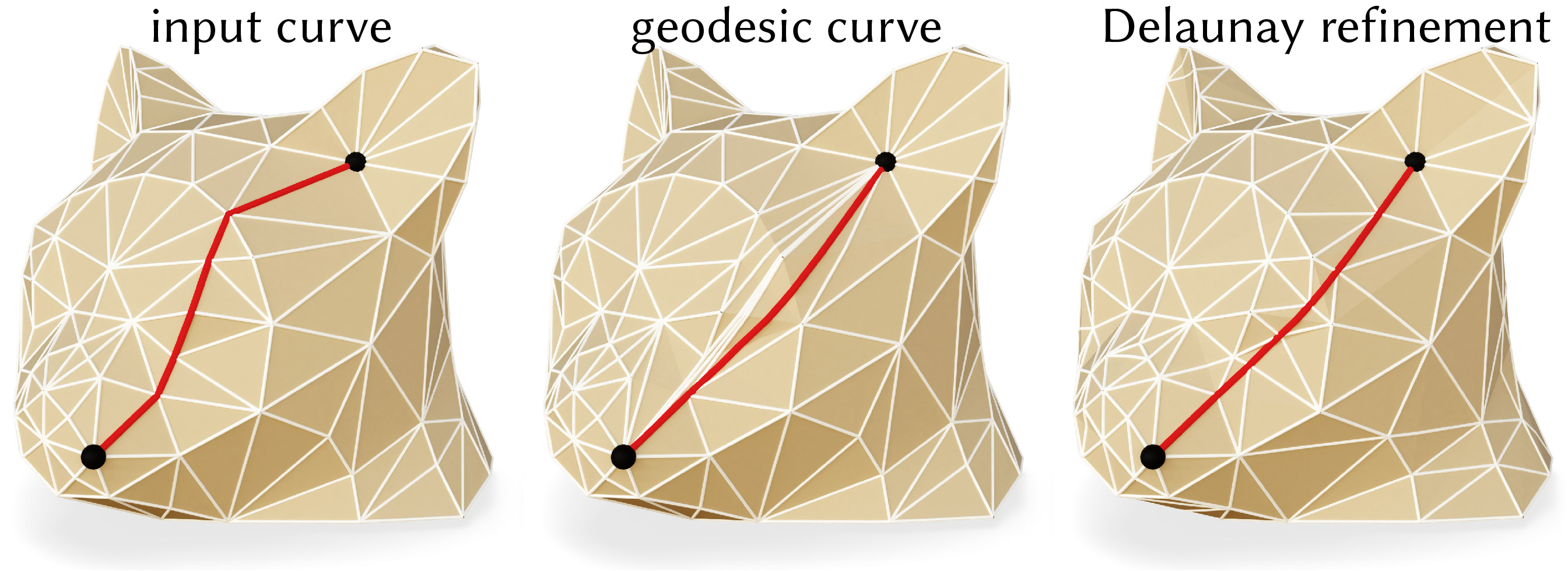
Improving the triangulation
As noted above, we can additionally generate a triangulation which conforms to geodesic curves, but this triangulation will often contain extremely skinny triangles. Performing Delaunay refinement improves the triangle quality for subsequent computation.
void FlipEdgeNetwork::delaunayRefine(double areaThresh = std::numeric_limits<double>::infinity(), size_t maxInsertions = INVALID_IND, double angleBound = 25.)
Perform intrinsic Delaunay refinement on the underlying triangulation to improve its numerical quality while preserving the geodesics.
Additional arguments are as in SignpostIntrinsicTriangulation::delaunayRefine().
Output and utilities
After running iterativeShorten(), the resulting geodesic paths are represented as a collection edges in an updated intrinsic triangulation. The most common operation is to extract the resulting path network as a polyline along the surface. Note that these routines return a double list; the outer list represents the paths/loops in the network, while the inner list are the points in each path/loop.
One option is to get the output as a sequence of surface points, where each is a vertex or a point along some edge in the mesh.
std::vector<std::vector<SurfacePoint>> FlipEdgeNetwork::getPathPolyline()
Get the path network as a sequence of surface points along the input mesh.
std::vector<std::vector<SurfacePoint>> FlipEdgeNetwork::getAllEdgePolyline()
Get all edges in the underlying triangulation as a sequence of surface points along the input mesh.
A simpler approach is to simply extract the path as a sequence of points in 3D space.
To use this approach, you must first set your 3D mesh geometry as the posGeom member. This extra step is necessary because in general, the FlipEdgeNetwork can be applied to meshes which have only edge lengths, but extracting 3D points requires your mesh to have 3D positions. (see the example at the top.)
std::vector<std::vector<Vector3>> FlipEdgeNetwork::getPathPolyline3D()
Get the path network as a sequence of points in 3D space.
To use this approach, you must first set your 3D mesh geometry as the posGeom member.
std::vector<std::vector<Vector3>> FlipEdgeNetwork::getAllEdgePolyline3D()
Get all edges in the underlying intrinsic triangulation as a sequence of points in 3D space.
To use this approach, you must first set your 3D mesh geometry as the posGeom member.
Additionally, a collection of useful utility functions are provided (see flip_geodesic.h the complete listing).
void FlipEdgeNetwork::rewind()
Undo any flips which have been performed, resetting the data structure to its initial state.
Note that you must set FlipEdgeNetwork::supportRewinding = true right after constructure (before doing any shortening) to be able to use rewind().
bool FlipEdgeNetwork::edgeInPath(Edge e)
Test whether a given edge from the intrinsic triangulation appears in the path.
bool FlipEdgeNetwork::halfedgeInPath(Halfedge he)
Test whether a given halfedge from the intrinsic triangulation appears in the path.
double FlipEdgeNetwork::length()
Measure the total length of the path network.
double FlipEdgeNetwork::minAngleIsotopy()
Measure the smallest angle in the path (not blocked by isotopy, aka the constraint that curves do not cross).
void FlipEdgeNetwork::savePathOBJLine(std::string filenamePrefix, bool withAll = false)
Write the path to file as line entries in an obj file.
Citation
If these routines contribute to academic work, please cite:
@article{sharp2020you,
title={You can find geodesic paths in triangle meshes by just flipping edges},
author={Sharp, Nicholas and Crane, Keenan},
journal={ACM Transactions on Graphics (TOG)},
volume={39},
number={6},
pages={1--15},
year={2020},
publisher={ACM New York, NY, USA}
}