Heat distance and transport on general polygon meshes
Compute signed and unsigned geodesic distance, and transport tangent vectors using fast solvers based on short-time heat flow.
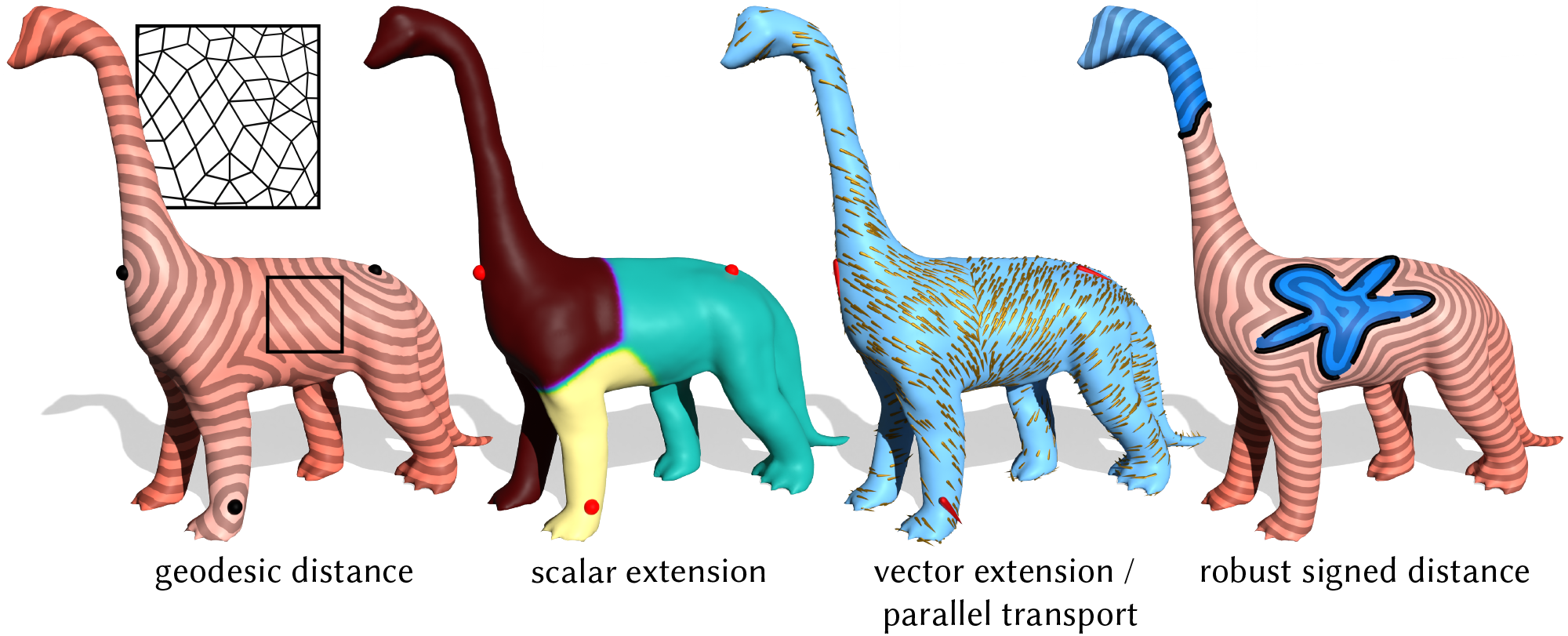
These routines implement polygon mesh versions of the algorithms from:
- The Heat Method for Distance Computation (distance)
- The Vector Heat Method (parallel transport)
- A Heat Method for Generalized Signed Distance (signed distance)
All computation is encapsulated by the PolygonMeshHeatSolver class, which maintains prefactored linear systems for the various methods. Some setup work is performed both on construction, and after the first query. Subsequent queries, even with different source points, will be fast.
#include "geometrycentral/surface/polygon_mesh_heat_solver.h"
For the original algorithms on triangle meshes, see the documentation for the Unsigned Heat Method, Vector Heat Method, and Signed Heat Method.
Example: Basic usage
#include "geometrycentral/surface/polygon_mesh_heat_solver.h"
using namespace geometrycentral;
using namespace geometrycentral::surface;
// Read in a polygon mesh
std::unique_ptr<SurfaceMesh> mesh;
std::unique_ptr<VertexPositionGeometry> geom;
std::tie(mesh, geom) = readSurfaceMesh("my_mesh.obj");
// Create the solver
PolygonMeshHeatSolver solver(*geom);
// Pick a source point or two
Vertex vSource = mesh->vertex(7);
Vertex vSource2 = mesh->vertex(8);
// Pick some source curves
std::vector<std::vector<Vertex>> curves;
curves.push_back({mesh->vertex(11), mesh->vertex(12), mesh->vertex(15), mesh->vertex(14), mesh->vertex(13)});
curves.push_back({mesh->vertex(17), mesh->vertex(18), mesh->vertex(19)});
// Compute geodesic distance
VertexData<double> distance = solver.computeDistance(vSource);
// Compute signed distance to a set of curves.
VertexData<double> signedDistance = solver.computeSignedDistance(curves);
// Compute scalar extension
VertexData<double> extended = solver.extendScalars({{vSource, 3.},
{vSource2, -5.}});
// Compute parallel transport
Vector2 sourceVec{1, 2};
VertexData<Vector2> transport = solver.transportTangentVector(vSource, sourceVec);
Constructor
PolygonMeshHeatSolver::PolygonMeshHeatSolver(EmbeddedGeometryInterface& geom, double tCoef = 1.0)
Create a new solver for the heat methods. Precomputation is performed at startup and lazily as needed.
-
geomis the geometry (and hence mesh) on which to compute. Any embedded geometry object (VertexPositionGeometry, etc) can be passed here. -
tCoefis the time to use for short time heat flow, as a factorm * h^2, wherehis the maximum between-point spacing. The default value of1.0is almost always sufficient.
Algorithm options (like tCoef) cannot be changed after construction; create a new solver object with the new settings.
Geodesic distance
Geodesic distance is the distance from a given source along the surface represented by the point cloud. Specifying multiple source points yields the distance to the nearest source.
VertexData<double> PolygonMeshHeatSolver::computeDistance(const Vertex& sourceVert)
Compute the geodesic distance from sourceVert to all other points.
VertexData<double> PolygonMeshHeatSolver::computeDistance(const std::vector<Vertex>& sourceVerts)
Like above, but for multiple source points.
Signed geodesic distance
VertexData<double> PolygonMeshHeatSolver::computeSignedDistance(const std::vector<std::vector<Vertex>>& curves, const LevelSetConstraint& levelSetConstraint = LevelSetConstraint::ZeroSet)
Compute the signed geodesic distance from a set of curves curves to all other points. Each curve in curves is a single connected component specified as an ordered sequence of points; curve orientations are derived from this order. The argument levelSetConstraint can be set to LevelSetConstraint::ZeroSet, LevelSetConstraint::Multiple, or LevelSetConstraint::None, corresponding to preservation of curves as the zero set, as multiple level sets (one for each curve component), or no constraint, respectively.
Scalar extension
Given scalar values defined at isolated vertices in the domain, extend it to a scalar field on all vertices. Each point will take the value from the nearest source point, in the sense of geodesic distance. Note that the fast diffusion algorithm means the result is a slightly smoothed-out field.
VertexData<double> PolygonMeshHeatSolver::extendScalars(const std::vector<std::tuple<Vertex, double>>& sources)
Given a collection of source vertices and scalars at those vertices, extends the scalar field to the whole mesh as a nearest-geodesic-neighbor interpolant.
Vector extension
Given tangent vectors defined at one or more isolated source locations on a surface, extend transport the vectors across the entire domain according to parallel transport. Each point on the domain will take the value of the nearest source point. Note that the fast diffusion algorithm means the result is a slightly smoothed-out field.
VertexData<Vector2> PolygonMeshHeatSolver::transportTangentVector(const Vertex& sourceVert, const Vector2& sourceVector)
Shorthand for the general version below when there is just one vector.
Computes parallel transport of the given vector along shortest geodesics to the rest of the domain.
Polar directions are defined in each vertex’s tangent space. See EmbeddedGeometryInterface::vertexTangentBasis.
VertexData<Vector2> PolygonMeshHeatSolver::transportTangentVectors(const std::vector<std::tuple<Vertex, Vector2>>& sources)
Given a collection of source vertices and tangent vectors at those vertices, extends the vector field to the whole domain as a nearest-geodesic-neighbor interpolant via parallel transport along shortest geodesics.
Polar directions are defined in each vertex’s tangent space. See EmbeddedGeometryInterface::vertexTangentBasis.