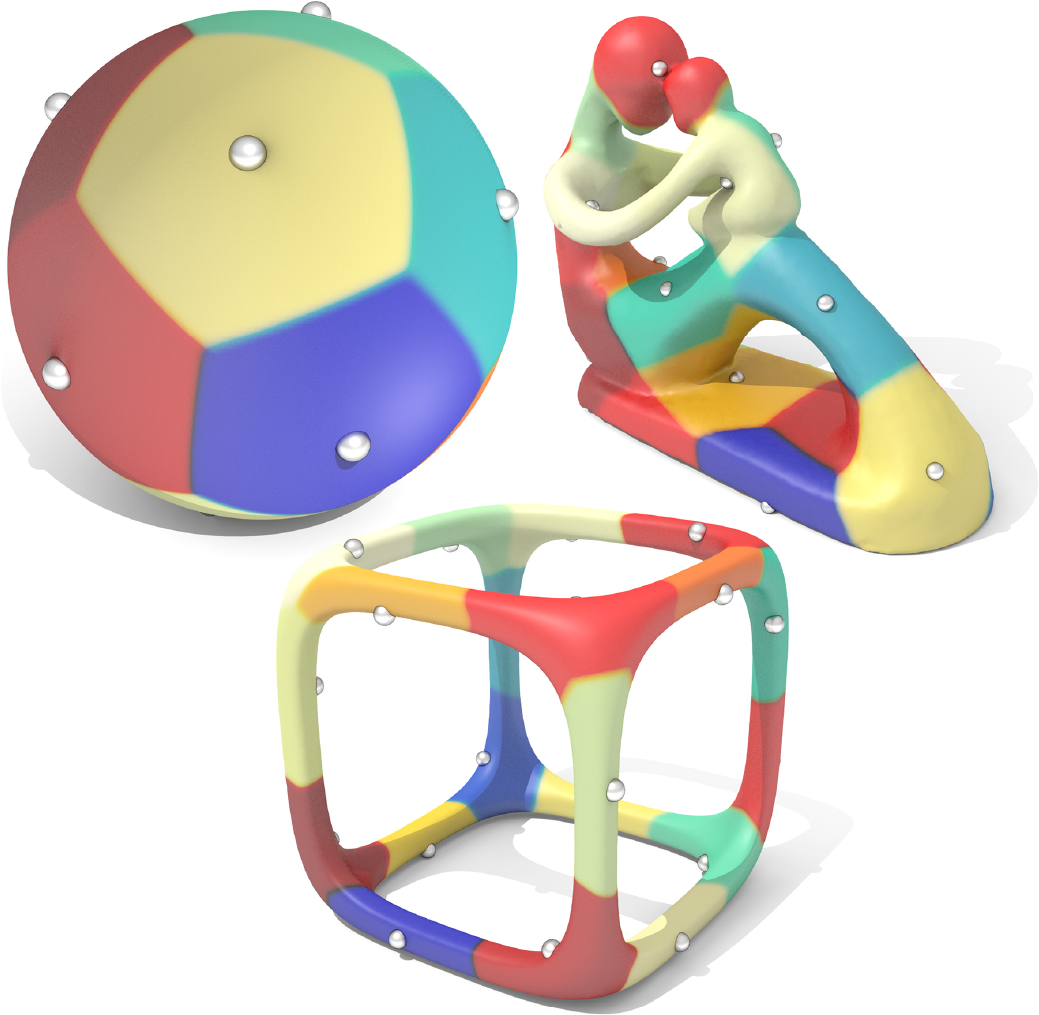
Geodesic Centroidal Voronoi Tessellations

A Voronoi tessellation partitions a domain $M$ based on a set of sites $s_i \in M$ . To each site $s_i$ , we associate a region (or “Voronoi cell”) consisting of the points closer to $s_i$ than to any other site. Such a tessellation is called centroidal if each site is at the center of its corresponding cell. This routine computes centroidal Voronoi tessellations on surface meshes.

Output is not unique!

By default, this procedure picks some random points and optimizes them to compute a centroidal Voronoi tessellation. Since the initialization is random, the results will generally be different each time the procedure is run.

#include "geometrycentral/surface/geodesic_centroidal_voronoi_tessellation.h"

karcher means

VoronoiResult computeGeodesicCentroidalVoronoiTessellation(ManifoldSurfaceMesh& mesh, IntrinsicGeometryInterface& geom, VoronoiOptions options = defaultVoronoiOptions)

Compute a geodesic centroidal Voronoi tessellation on the input mesh. Options are passed as a VoronoiOptions object, and the output is returned as a VoronoiResult object.

Helper Types

Options

Options are passed in to computeGeodesicCentroidalVoronoiTessellation via a VoronoiOptions object.

Field	Default value	Meaning
`size_t nSites;`	`10`	the number of sites to place
`std::vector<SurfacePoint> initialSites;`	`{}`	desired locations for sites. If blank, initial locations are chosen randomly
`size_t iterations;`	`50`	number of iterations to run for
`bool useDelaunay;`	`true`	solve on an intrinsic Delaunay triangulation of the input
`double tCoef;`	`1`	diffusion time for the vector heat method
`size_t nSubIterations;`	`1`	number of iterations to use when computing surface centers during optimization

Result

The result is returned as a VoronoiResult, which has 3 fields:

Field	Meaning
`std::vector<SurfacePoint> siteLocations;`	the sites at the centers of the Voronoi cells
`std::vector<VertexData<double>> siteDistributions;`	indicator functions which each Voronoi cell
`bool hasDistributions;`	is `siteDistributions` populated?

Citation

This algorithms is described in The Vector Heat Method, the appropriate citation is:

@article{sharp2019vector,
  title={The Vector Heat Method},
  author={Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
  journal={ACM Transactions on Graphics (TOG)},
  volume={38},
  number={3},
  pages={24},
  year={2019},
  publisher={ACM}
}