Surface Centers

These routines compute geometric centers of point sets and distrubtions on surfaces.

A “center” $c$ is a point on the surface which is a local minimum of the energy: $$ c = \underset{m}{\textrm{argmin}}\sum_{y \in \mathcal{Y}} d(m,y)^p $$ where $\mathcal{Y}$ is a set of sites to take the average of and $d(\cdot, \cdot)$ denotes the geodesic distance.

Centers on surfaces with $p=2$ (“means”) are known as Karcher Means or Frechet Means. Centers on surfaces with $p=1$ (“medians”) are known as geometric medians.

Centers are not unique!

In general, there will not be a single unqiue “center” of a point set or distribution on a surface. For nearby sites there may be a single center, but in general this may not be the case.

The routines in this section use random initialization to report a center. As such, the results may be different under repeated runs of the procedure.

#include "geometrycentral/surface/surface_centers.h"

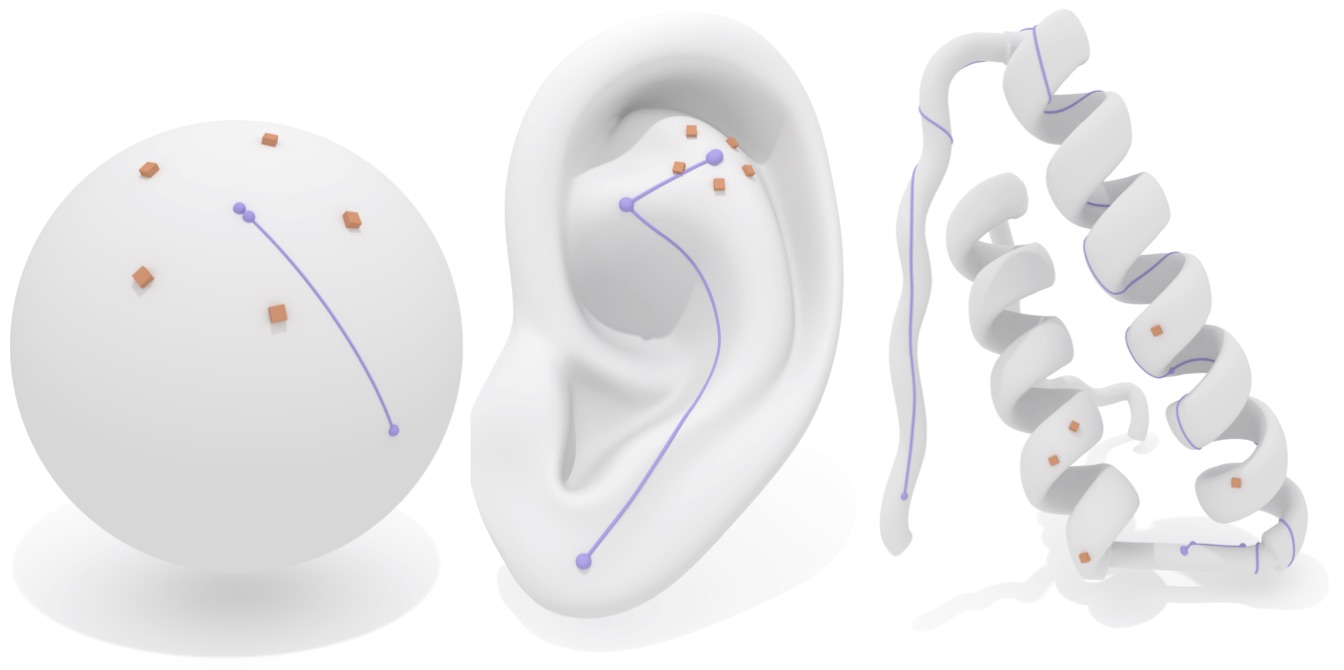
karcher means

Centers of points

SurfacePoint findCenter(IntrinsicGeometryInterface& geom, const std::vector<Vertex>& vertexPts, int p = 2)

Find a center of a collection of points at vertices.

p must be either $1$ or $2$ .

SurfacePoint findCenter(IntrinsicGeometryInterface& geom, VectorHeatMethodSolver& solver, const std::vector<Vertex>& vertexPts, int p = 2)

Like the above method, but uses an existing solver object, which saves precomputation.

Centers of distributions

SurfacePoint findCenter(IntrinsicGeometryInterface& geom, const VertexData<double>& distribution, int p = 2)

Find a center of a distribution at vertices.

Note that the input distribution is treated as integrated values at vertices. If your distribution is “per-unit-area”, you should multiply times vertex area before passing it in.

p must be either $1$ or $2$ .

SurfacePoint findCenter(IntrinsicGeometryInterface& geom, VectorHeatMethodSolver& solver, const VertexData<double>& distribution, int p = 2)

Like the above method, but uses an existing solver object, which saves precomputation.

Citation

These algorithms are described in The Vector Heat Method, the appropriate citation is:

@article{sharp2019vector,
  title={The Vector Heat Method},
  author={Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
  journal={ACM Transactions on Graphics (TOG)},
  volume={38},
  number={3},
  pages={24},
  year={2019},
  publisher={ACM}
}