Quantities

This page enumerates the surface geometry quantities available in geometry central.

Recall that these quantities are each associated with a geometry interface specifying what can be computed from the given input data. Instantiating a geometry from data, classes like VertexPositionGeometry extend these interfaces and give access to all of the quantities therein. Quantities should usually be accessed via the managed caches, as in the example below.

#include "geometrycentral/surface/vertex_position_geometry.h"
#include "geometrycentral/surface/meshio.h"
using namespace geometrycentral::surface;

// Load a mesh and geometry from file
std::unique_ptr<SurfaceMesh> mesh;
std::unique_ptr<VertexPositionGeometry> positionGeometry;
std::tie<mesh, positionGeometry> = readSurfaceMesh("spot.obj");

// For the sake of the example, use an interface type that offers
// only the quantities which we will actually use below.
IntrinsicGeometryInterface& geometry = *positionGeometry;

// populate the quantity
geometry.requireFaceAreas();

for(Face f : mesh->faces()) {

  // Managed array holding quantity
  double area = geometry.faceAreas[f];

  // Immediate computation, computes directly from 
  // input data without touching caches.
  // Generally discouraged but occasionally useful.
  area = positionGeometry->faceArea(f);
}

Indices

These quantities are defined for the base BaseGeometryInterface, and will always be available. They are not actually geometric data, but it is convenient to cache the canonical arrays alongside geometric quantities, as they are often used in concert.

vertex indices

A dense 0-based enumeration of vertices. Equivalent to the result of SurfaceMesh::getVertexIndices().

member: VertexData<size_t> BaseGeometryInterface::vertexIndices
require: void BaseGeometryInterface::requireVertexIndices()

halfedge indices

A dense 0-based enumeration of halfedges. Equivalent to the result of SurfaceMesh::getHalfedgeIndices().

member: HalfedgeData<size_t> BaseGeometryInterface::halfedgeIndices
require: void BaseGeometryInterface::requireHalfedgeIndices()

corner indices

A dense 0-based enumeration of corners. Equivalent to the result of SurfaceMesh::getCornerIndices().

member: CornerData<size_t> BaseGeometryInterface::cornerIndices
require: void BaseGeometryInterface::requireCornerIndices()

edge indices

A dense 0-based enumeration of edges. Equivalent to the result of SurfaceMesh::getEdgeIndices().

member: EdgeData<size_t> BaseGeometryInterface::edgeIndices
require: void BaseGeometryInterface::requireEdgeIndices()

face indices

A dense 0-based enumeration of faces. Equivalent to the result of SurfaceMesh::getFaceIndices().

member: FaceData<size_t> BaseGeometryInterface::faceIndices
require: void BaseGeometryInterface::requireFaceIndices()

boundary loop indices

A dense 0-based enumeration of boundary loops. Equivalent to the result of SurfaceMesh::getBoundaryLoopIndices().

member: BoundaryLoopData<size_t> BaseGeometryInterface::boundaryLoopIndices
require: void BaseGeometryInterface::requireBoundaryLoopIndices()

Lengths, areas, and angles

These quantities are defined for any IntrinsicGeometryInterface, which is the base class of all other geometry objects—they will always be available on any kind of geometry.

edge length

The length of an edge in the mesh, as a non-negative real number.

member: EdgeData<double> IntrinsicGeometryInterface::edgeLengths
require: void IntrinsicGeometryInterface::requireEdgeLengths()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: double VertexPositionGeometry::edgeLength(Edge e)

face area

The area of a face, as a non-negative real number.

May be computed from edge lengths via Heron’s formula, or from embedded vertex positions with a cross product.

Only valid on triangular meshes.

member: FaceData<double> IntrinsicGeometryInterface::faceAreas
require: void IntrinsicGeometryInterface::requireFaceAreas()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: double EdgeLengthGeometry::faceArea(Face f)
immediate: double VertexPositionGeometry::faceArea(Face f)

vertex dual area

An area associated with each vertex, as a non-negative real number.

Only valid on triangular meshes.

Defined to be $1/3$ the sum of all adjacent face areas. The sum of all vertex dual areas is equal to the usual surface area of the mesh.

member: VertexData<double> IntrinsicGeometryInterface::vertexDualAreas
require: void IntrinsicGeometryInterface::requireVertexDualAreas()

The inline immediate method can be used to compute this value directly from input data for a single element:

immediate: double EdgeLengthGeometry::vertexDualArea(Vertex v)
immediate: double VertexPositionGeometry::vertexDualArea(Vertex v)

corner angles

The angle between incident edges at each corner of a mesh.

Only valid on triangular meshes.

member: CornerData<double> IntrinsicGeometryInterface::cornerAngles
require: void IntrinsicGeometryInterface::requireCornerAngles()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: double EdgeLengthGeometry::cornerAngle(Corner c)
immediate: double VertexPositionGeometry::cornerAngle(Corner c)

vertex angle sum

The sum of corner angles around a vertex.

Only valid on triangular meshes.

member: VertexData<double> IntrinsicGeometryInterface::vertexAngleSums
require: void IntrinsicGeometryInterface::requireVertexAngleSums()

corner scaled angles

The angle between incident edges at each corner of a mesh, linearly rescaled such that the angles around every vertex sum to $2 \pi$ . At boundary vertices, no scaling will be performed.

Only valid on triangular meshes.

member: CornerData<double> IntrinsicGeometryInterface::cornerScaledAngles
require: void IntrinsicGeometryInterface::requireCornerScaledAngles()

halfedge cotan weight

The “cotangent weight” of an interior halfedge, defined as $\frac{1}{2} \cot(\theta)$ , where $\theta$ is the corner angle opposite the halfedge. Defined to be $0$ for exterior halfedges.

Can be computed directly from edge lengths, or more efficiently in an embedded triangle via $\cot(\theta) = \frac{u \cdot v}{||u \times v||}$ , where $u$ and $v$ are the edge vectors emanating from the opposite corner.

Only valid on triangular meshes.

member: HalfedgeData<double> IntrinsicGeometryInterface::halfedgeCotanWeights
require: void IntrinsicGeometryInterface::requireHalfedgeCotanWeights()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: double EdgeLengthGeometry::halfedgeCotanWeight(Halfedge he)
immediate: double VertexPositionGeometry::halfedgeCotanWeight(Halfedge he)

edge cotan weight

The “cotangent weight” of an edge, defined as the sum of halfedge cotan weights for incident interior halfedges.

Only valid on triangular meshes.

member: EdgeData<double> IntrinsicGeometryInterface::edgeCotanWeights
require: void IntrinsicGeometryInterface::requireEdgeCotanWeights()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: double EdgeLengthGeometry::edgeCotanWeight(Edge e)
immediate: double VertexPositionGeometry::edgeCotanWeight(Edge e)

Curvatures

Different curvatures are available depending on whether geometry is intrinsic or extrinsic. In particular, Gaussian curvature is available for any IntrinsicGeometryInterface (such as EdgeLengthGeometry), which is the base class of all other geometry objects, whereas mean and principal curvatures are available only from an ExtrinsicGeometryInterface (such as VertexPositionGeometry). All curvatures are rigid motion invariant. Importantly, Gaussian and mean curvatures correspond to the integral of curvature over a local neighborhood, and are hence scale invariant—to get the pointwise curvatures you should divide by area (see details below). Principal curvatures are pointwise values. See also vertexPrincipalCurvatureDirections, which provides curvature directions (rather than curvature magnitudes). See this video for further background on discrete curvature.

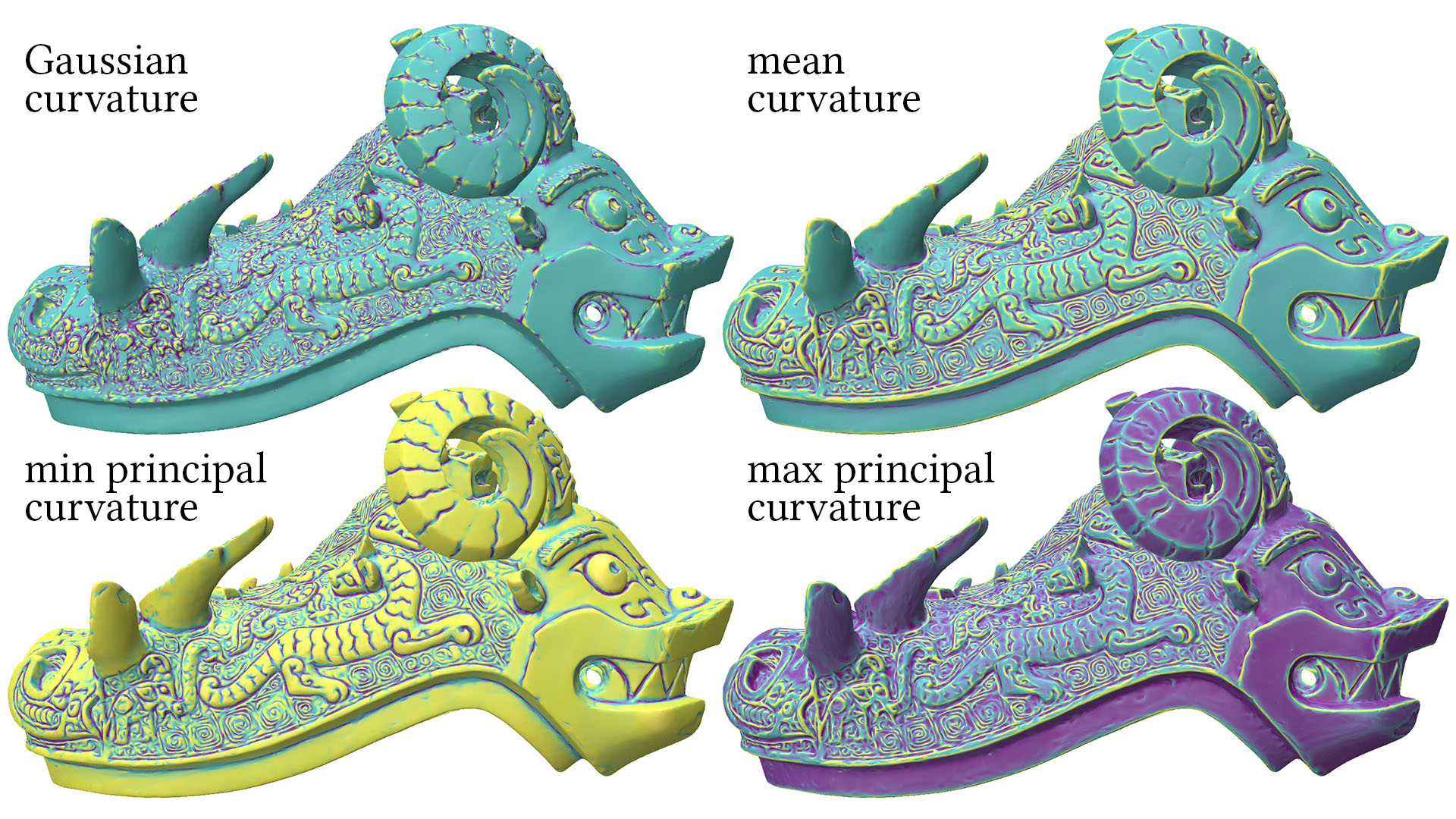
vertex scalar curvatures

vertex Gaussian curvature

The Gaussian curvature $K$ at a vertex, defined via the angle defect $K_v = 2 \pi - \sum \theta_i$ , where $\sum \theta_i$ is the vertexAngleSum as above.

Should be interpreted as an integrated Gaussian curvature, giving the total curvature in the neighborhood of the vertex. On a closed surface, the Gauss-Bonnet theorem tells us that the sum of these Gaussian curvatures will be a topological constant given by $\sum_v K_v = 2 \pi \chi$ , where $\chi$ is the Euler characteristic of the surface. On surfaces with boundary, the geodesic curvature of the boundary factors in.

Only valid on triangular meshes.

member: VertexData<double> IntrinsicGeometryInterface::vertexGaussianCurvatures
require: void IntrinsicGeometryInterface::requireVertexGaussianCurvatures()

The inline immediate method can be used to compute this value directly from input data for a single element:

immediate: double VertexPositionGeometry::vertexGaussianCurvature(Vertex v)
immediate: double EdgeLengthGeometry::vertexGaussianCurvature(Vertex v)

vertex mean curvature

The mean curvature $H$ at a vertex $i$ , defined via the Steiner approximation $H_i = \frac{1}{4}\sum_{ij} \theta_{ij} \ell_{ij}$ , where $\theta_{ij}$ is the edgeDihedralAngle and $\ell_{ij}$ is the edgeLength as defined above (and the sum is taken over halfedges extending from $i$ ).

Should be interpreted as an integrated mean curvature (units: $m$ ), giving the total curvature in the neighborhood of the vertex. A corresponding pointwise mean curvature (units: $1/m$ ) can be obtained by dividing by the vertexDualArea.

Only valid on triangular meshes.

member: VertexData<double> ExtrinsicGeometryInterface::vertexMeanCurvatures
require: void ExtrinsicGeometryInterface::requireVertexMeanCurvatures()

The inline immediate method can be used to compute this value directly from input data for a single element:

immediate: double VertexPositionGeometry::vertexMeanCurvature(Vertex v)

vertex principal curvature

vertex principal curvatures

The principal curvatures $\kappa_1,\kappa_2$ at a vertex $i$ , defined by the relationships $K = \kappa_1\kappa_2$ and $H = (\kappa_1+\kappa_2)/2$ , where $H$ and $K$ are the pointwise mean and Gaussian curvatures (resp.). These values are signed, and $\kappa_1$ is always the smaller curvature in value, but not necessarily the smaller one in magnitude (e.g., $\kappa_1$ could be a very large negative value, and $\kappa_2$ could be a very small positive value).

These quantities can be interpreted as pointwise quantities (units: $1/m$ ), approximating the maximum and minimum bending the neighborhood of the vertex.

Only valid on triangular meshes.

member: VertexData<double> ExtrinsicGeometryInterface::vertexMinPrincipalCurvatures
require: void ExtrinsicGeometryInterface::requireVertexMinPrincipalCurvatures()
member: VertexData<double> ExtrinsicGeometryInterface::vertexMaxPrincipalCurvatures
require: void ExtrinsicGeometryInterface::requireVertexMaxPrincipalCurvatures()

The inline immediate methods can be used to compute this value directly from input data for a single element:

immediate: double VertexPositionGeometry::vertexMinPrincipalCurvature(Vertex v)
immediate: double VertexPositionGeometry::vertexMaxPrincipalCurvature(Vertex v)

face Gaussian curvature

The Gaussian curvature $K$ at a face, defined via the rescaled angle defect in the face $K_f = \pi - \sum \tilde{\theta}_i$ , where $\tilde{\theta}_i$ are the rescaled corner angles (as in cornerScaledAngles) incident on the face.

Should be interpreted as an integrated Gaussian curvature, giving the total curvature inside of the face. A corresponding curvature-per-unit-area can be computed by dividing by the area of the face.

On a closed surface, the Gauss-Bonnet theorem tells us that the sum of these Gaussian curvatures will be a topological constant given by $\sum_f K_f = 2 \pi \chi$ , where $\chi$ is the Euler characteristic of the surface. On surfaces with boundary, the geodesic curvature of the boundary factors in.

Only valid on triangular meshes.

member: FaceData<double> IntrinsicGeometryInterface::faceGaussianCurvatures
require: void IntrinsicGeometryInterface::requireFaceGaussianCurvatures()

Tangent vectors and transport

These quantities are defined for any IntrinsicGeometryInterface, which is the base class of all other geometry objects—they will always be available on any kind of geometry. Tangent vectors and transport are defined in terms of tangent spaces at faces and vertices, as defined below.

Recall that our Vector2 types obey the multiplication and division rules of complex arithmetic, and thus can be used to represent rotations. For instance, a 2D vector representing a rotation can be used to rotate another vector like:

Vector2 v = /* your vector */
Vector2 r = Vector2{std::cos(PI/4), std::sin(PI/4)}; // rotation by 45 degrees
Vector2 vRot = r * v;

This is fundamentally no different from using 2x2 rotation matrices, but leads to much cleaner code (try using division to compute relative rotations!).

Face tangent spaces

To represent vectors that sit in flat mesh faces, we define a 2D coordinate frame tangent to each face. By default, this frame is aligned such that face.halfedge() points along the $x$ -axis (but subclasses might change this convention). All vectors in faces are then expressed via $(x,y)$ Vector2D coordinates in this frame. Crucially, this basis is well-defined even if the geometry does not have vertex positions.

See face tangent basis to convert these vectors to world coordinates (if your mesh has vertex positions).

halfedge vectors in face

Vectors for each halfedge in the coordinate frame of the face in which they sit. See the description of face tangent spaces above for a definition.

Only valid on triangular meshes.

member: HalfedgeData<Vector2> IntrinsicGeometryInterface::halfedgeVectorsInFace
require: void IntrinsicGeometryInterface::requireHalfedgeVectorsInFace()

transport vector across halfedge

Rotations which transport tangent vectors across a halfedge, rotating a vector from the tangent space of halfedge.face() to the tangent space halfedge.twin().face().

Always a unit vector, which can be multiplied by any other vector to compute the rotation. (recall our Vector2s multiply like complex numbers)

Only valid on triangular meshes. Not defined for halfedges (interior or exterior) incident on boundary edges, these boundary values are set to NaN so errors can be caught quickly.

member: HalfedgeData<Vector2> IntrinsicGeometryInterface::transportVectorsAcrossHalfedge
require: void IntrinsicGeometryInterface::requireTransportVectorAcrossHalfedge()

Example usage:

geometry.requireTransportVectorsAcrossHalfedge();

Face f = /* ... */;        // a face of interest
Vector2 myVec = /* ... */; // tangent vector in face f

for(Halfedge he : f.adjacentHalfedges()) {

  Face neighborFace = he.twin().face();
  Vector2 rot = geometry.transportVectorAcrossHalfedge[he];
  Vector2 neighVec = rot * myVec;    // now in the basis of neighborFace
}

Vertex tangent spaces

To represent vectors that sit at mesh faces, we consider a polar coordinate frame at each vertex. This frame is defined by measuring angles according to the rescaled corner angles as in cornerScaledAngles. By default, this frame is aligned such that vertex.halfedge() points along the $\phi=0$ $x$ -axis (but subclasses might change this convention). Of course, rather than using polar coordinates we can equivalently work in the corresponding Cartesian frame—tangent vectors at vertices are then expressed via $(x,y)$ Vector2D coordinates in this frame. Crucially, this basis does not require picking a vertex normal, and is well-defined even if the geometry does not have vertex positions.

See vertex tangent basis to convert these tangent vectors to world coordinates (if your mesh has vertex positions).

vertex tangent coordinates diagram

halfedge vectors in vertex

Vectors for each halfedge in the coordinate frame of the vertex from which the emanate (in halfedge.vertex()). See the description of vertex tangent spaces above for a definition.

Only valid on triangular meshes.

member: HalfedgeData<Vector2> IntrinsicGeometryInterface::halfedgeVectorsInVertex
require: void IntrinsicGeometryInterface::requireHalfedgeVectorsInVertex()

transport vector along halfedge

Rotations which transport tangent vectors along a halfedge, rotating a vector from the tangent space of halfedge.vertex() to the tangent space halfedge.twin().vertex().

Always a unit vector, which can be multiplied by any other vector to compute the rotation. (recall our Vector2s multiply like complex numbers)

Only valid on triangular meshes.

member: HalfedgeData<Vector2> IntrinsicGeometryInterface::transportVectorsAlongHalfedge
require: void IntrinsicGeometryInterface::requireTransportVectorsAlongHalfedge()

Example usage:

geometry.requireTransportVectorsAlongHalfedge();

Vertex v = /* ... */;        // a vertex of interest
Vector2 myVec = /* ... */;   // tangent vector in vertex v

for(Halfedge he : v.outgoingHalfedges()) {
  Vertex neighborVertex = he.twin().vertex();
  Vector2 rot = geometry.transportVectorAlongHalfedge[he];
  Vector2 neighVec = rot * myVec;    // now in the basis of neighborVertex
}

Operators

These quantities are defined for any IntrinsicGeometryInterface, which is the base class of all other geometry objects—they will always be available on any kind of geometry. A full explanation of these operators is beyond the scope of these docs; see these course notes for one introduction.

All operators are indexed over mesh elements according to the natural iteration order of the elements, or equivalently the indices from SurfaceMesh::getVertexIndices() (etc).

cotangent Laplacian

cotangent laplacian

The discrete Laplace operator, discretized via cotangent weights.

A $|V| \times |V|$ real matrix. Always symmetric and positive semi-definite. If and only the underlying geometry is Delaunay, the matrix will furthermore have all negative off-diagonal entries, satisfy a maximum principle, and be an M-matrix.

This is the weak Laplace operator, if we use it to evalutae $\mathsf{y} \leftarrow \mathsf{L} \mathsf{x}$ , $\mathsf{x}$ should hold pointwise quantities at vertices, and the result $\mathsf{y}$ will contain integrated values of the result in the neighborhood of each vertex. If used to solve a Poisson problem, a mass matrix (such as the lumped or Galerkin mass matrices below) are likely necessary on the right hand side.

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::cotanLaplacian
require: void IntrinsicGeometryInterface::requireCotanLaplacian()

vertex lumped mass matrix

A mass matrix at vertices, where vertex area is $1/3$ the incident face areas as in vertexDualAreas.

A $|V| \times |V|$ real diagonal matrix. Generally less-accurate than the Galerkin mass matrix below, but can be easily inverted since it is a diagonal matrix.

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::vertexLumpedMassMatrix
require: void IntrinsicGeometryInterface::requireVertexLumpedMassMatrix()

vertex Galerkin mass matrix

A mass matrix at vertices, supported at all neighbors of a vertex via integration of piecewise-linear elements.

A $|V| \times |V|$ real matrix. Generally more accurate than the lumped mass matrix above, should be preferred unless the mass matrix needs to be inverted.

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::vertexGalerkinMassMatrix
require: void IntrinsicGeometryInterface::requireVertexGalerkinMassMatrix()

vertex connection Laplacian

A discrete connection Laplacian operator, which applies to vector fields defined in vertex tangent spaces. Essentially defined as the scalar cotangent Laplacian, augmented with rotations given by the rotations in transportVectorAlongHalfedge; see The Vector Heat Method, Sec 5.3 for more explanation and definition.

A $|V| \times |V|$ complex matrix. Always Hermitian, but positive semi-definite if and only the underlying geometry is Delaunay. This is a weak Laplace operator, the application of which outputs integrated values in vertex neighborhood.

Given a complex vector $\mathsf{x}$ of tangent vectors at vertices, apply the operator by multiplying $\mathsf{L} * \mathsf{x}$ .

Only valid on triangular meshes.

member: Eigen::SparseMatrix<std::complex<double>> IntrinsicGeometryInterface::vertexConnectionLaplacian
require: void IntrinsicGeometryInterface::requireVertexConnectionLaplacian()

DEC operators

These operators are the basic building blocks for discrete exterior calculus on surfaces.

Note: These quantities slightly deviate from the usual naming scheme for quantities. Rather than requireD0(), requireD1(), etc, there is a single requireDECOperators() function which manages all 8 of the members listed below.

The following members are constructed:

Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge0 A $|V| \times |V|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge0Inverse A $|V| \times |V|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge1 An $|E| \times |E|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge1Inverse An $|E| \times |E|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge2 An $|F| \times |F|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::hodge2Inverse An $|F| \times |F|$ diagonal matrix
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::d0 An $|E| \times |V|$ matrix with $\{-1, 0, 1\}$ entries
Eigen::SparseMatrix<double> IntrinsicGeometryInterface::d1 An $|F| \times |E|$ matrix with $\{-1, 0, 1\}$ entries

Only valid on triangular meshes.

require: void IntrinsicGeometryInterface::requireDECOperators()

While the vertex-based cotan Laplacian above is standard in geometry processing, one can also construct a discrete Laplacian using different basis functions. The following matrices are the result of using Crouzeix-Raviart basis functions, which are Lagrange elements based at edge midpoints: Each function is piecewise linear, has a value at 1 at its associated edge midpoint, and is 0 at all other adjacent edge midpoints.

In graphics and geometry processing, Crouzeix-Raviart elements have been used, for example, to discretize bending energies and discretize vector Dirichlet energy. Because there are typically more edges than vertices in a mesh, and there are only two faces in the support of each Crouzeix-Raviart basis function, Crouzeix-Raviart operators also typically have more DOFs than vertex-based operators.

Crouzeix-Raviart Laplacian

The discrete Laplace operator, discretized via the piecewise linear Crouzeix-Raviart basis functions associated with edge midpoints.

A $|E| \times |E|$ real matrix. Always symmetric and positive semi-definite. This is the weak Laplace operator, if we use it to evaluate $\mathsf{y} \leftarrow \mathsf{L} \mathsf{x}$ , $\mathsf{x}$ should hold pointwise quantities at edge midpoints, and the result $\mathsf{y}$ will contain integrated values of the result in the neighborhood of each edge midpoint. If used to solve a Poisson problem, a mass matrix is likely necessary on the right hand side.

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::crouzeixRaviartLaplacian
require: void IntrinsicGeometryInterface::requireCrouzeixRaviartLaplacian()

Crouzeix-Raviart mass matrix

A mass matrix at edges, where the edge area is $1/3$ the incident face areas.

A $|E| \times |E|$ real diagonal matrix. Corresponds to the Galerkin mass matrix for Crouzeix-Raviart elements, which is already diagonal without lumping.

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::crouzeixRaviartMassMatrix
require: void IntrinsicGeometryInterface::requireCrouzeixRaviartMassMatrix()

Crouzeix-Raviart connection Laplacian

A discrete connection Laplacian operator, which applies to vector fields defined in edge tangent spaces

A $|E| \times |E|$ complex matrix. Always Hermitian and positive semi-definite.

Given a complex vector $\mathsf{x}$ of tangent vectors at edge midpoints, apply the operator by multiplying $\mathsf{L} * \mathsf{x}$ . Like other mesh elements, the $x$ -axis of the tangent space at edge e points in the direction of e.halfedge().

Only valid on triangular meshes.

member: Eigen::SparseMatrix<double> IntrinsicGeometryInterface::crouzeixRaviartConnectionLaplacian
require: void IntrinsicGeometryInterface::requireCrouzeixRaviartConnectionLaplacian()

Extrinsic angles

These quantities depend on extrinsic angles, but are still rotation-invariant, and independent of a particular embeddeding. They are defined for ExtrinsicGeometryInterface and classes that extend it, including the EmbeddedGeometryInterface one usually constructs from vertex positions. Currently there is no realization that constructs an ExtrinsicGeometryInterface from input data which is not also an EmbeddedGeometryInterface, but such a class could be implemented in the future.

edge dihedral angle

The dihedral angle at an edge, in radians. Defined to be the signed angle between the incident triangle normals: $0$ if the edge is flat, positive at a convex edge, and negative at a nonconvex edge.

Only valid on triangular meshes.

member: EdgeData<double> ExtrinsicGeometryInterface::edgeDihedralAngles
require: void ExtrinsicGeometryInterface::requireEdgeDihedralAngles()

The inline immediate method can be used to compute this value directly from input data for a single element:

immediate: double VertexPositionGeometry::edgeDihedralAngle(Edge e)

vertex principal curvature direction

A 2-symmetric tangent vector field at vertices. The direction corresponds to the first principal direction, and the magnitude is proportional to the squared difference of the 1st and 2nd principal curvatures $(\kappa_1 - \kappa_2)^2$ (so for instance, if a surface is flat and $\kappa_1 \approx \kappa_2$ , the magnitude of the field will be near $0$ ).

A formal description appears in section 6.1.2 of Globally Optimal Direction Fields

Only valid on triangular meshes.

member: VertexData<Vector2> ExtrinsicGeometryInterface::vertexPrincipalCurvatureDirections
require: void ExtrinsicGeometryInterface::requireVertexPrincipalCurvatureDirections()

Embedded positions and normals

These quantities depend explicitly on an embedding in 3D space (better known as vertex positions). They are defined for EmbeddedGeometryInterface (which is usually instantiated as a VertexPositionGeometry). Don’t forget, EmbeddedGeometryInterface extends the IntrinsicGeometryInterface and ExtrinsicGeometryInterface, so all of the quantities above are also accessible.

vertex position

Vertex positions in 3D.

member: VertexData<Vector3> EmbeddedGeometryInterface::vertexPositions
require: void EmbeddedGeometryInterface::requireVertexPositions()

face normal

A normal vector for each face.

member: FaceData<Vector3> EmbeddedGeometryInterface::faceNormals
require: void EmbeddedGeometryInterface::requireFaceNormals()

The inline immediate method can alternately be used to compute this value directly from input data for a single element:

immediate: Vector3 VertexPositionGeometry::faceNormal(Face f)

vertex normal

A normal vector for each vertex. Defined as the corner-angle weighted average of incident face normals.

member: VertexData<Vector3> EmbeddedGeometryInterface::faceNormals
require: void EmbeddedGeometryInterface::requireFaceNormals()

vertex dual mean curvature normal

Conceptually, the mean curvature normal at any location on a surface is a vector which points in the normal direction, and has magnitude equal to the mean curvature at that location. In practice, we discretize this using the fact that applying the Laplacian to the position function yields the mean curvature normals.

Should be interpreted as an integrated mean curvature normal (units: $m$ ), giving the integral of the mean curvature curvature in the neighborhood of the vertex. A corresponding pointwise mean curvature (units: $1/m$ ) can be obtained by dividing by the vertexDualArea.

Only valid on triangular meshes.

member: VertexData<double> EmbeddedGeometryInterface::vertexDualMeanCurvatureNormals
require: void EmbeddedGeometryInterface::requireVertexDualMeanCurvatureNormals()

The inline immediate method can be used to compute this value directly from input data for a single element:

immediate: Vector3 VertexPositionGeometry::vertexDualMeanCurvatureNormal(Vertex v)

Fun fact: these vertex dual mean curvature normals are also the derivative of the mesh’s surface area with respect to vertex positions.

face tangent basis

A pair of $x$ -axis and $y$ -axis 3D basis vectors in world space, corresponding to the intrinsic tangent space for the face. Always orthogonal to the face normal.

Example:

SurfaceMesh& mesh = /* ... */ 
VertexPositionGeometry& geometry = /* ... */;    
FaceData<Vector2> myTangentVectorField;

geometry.requireFaceTangentBasis();

for(Face f : mesh.faces()) {
  Vector2 field = myTangentVectorField[f];

  Vector3 basisX = geometry.faceTangentBasis[f][0];
  Vector3 basisY = geometry.faceTangentBasis[f][1];

  Vector3 fieldInWorldCoords = basisX * field.x + basisY * field.y;
}

member: FaceData<std::array<Vector3,2>> EmbeddedGeometryInterface::faceTangentBasis
require: void EmbeddedGeometryInterface::requireFaceTangentBasis()

vertex tangent basis

A pair of $x$ -axis and $y$ -axis 3D basis vectors in world space, corresponding to the intrinsic tangent space for the vertex. Always orthogonal to the vertex normal.

Example:

SurfaceMesh& mesh = /* ... */ 
VertexPositionGeometry& geometry = /* ... */;    
VertexData<Vector2> myTangentVectorField;

geometry.requireFaceTangentBasis();

for(Vertex v : mesh.vertices()) {
  Vector2 field = myTangentVectorField[v];

  Vector3 basisX = geometry.vertexTangentBasis[v][0];
  Vector3 basisY = geometry.vertexTangentBasis[v][1];

  Vector3 fieldInWorldCoords = basisX * field.x + basisY * field.y;
}

member: VertexData<std::array<Vector3,2>> EmbeddedGeometryInterface::vertexTangentBasis
require: void EmbeddedGeometryInterface::requireVertexTangentBasis()