Skip to content

Vector Heat Method

This section describes the Vector Heat Method in geometry-central, which computes parallel transport of vectors using heat flow, and applications that follow from it.

Note that these quantities all depend on the intrinsic geometry of a surface (via the IntrinsicGeometryInterface). Therefore, these routines can be run on abstract geometric domains as well as traditional surfaces in 3D.

These algorithms are described in The Vector Heat Method and The Affine Heat Method.

#include "geometrycentral/surface/vector_heat_method.h"

For the polygon mesh version, see the polygon mesh heat solver; for point clouds, see the point cloud heat solver.

Vector Heat Solver

The stateful class VectorHeatSolver shares precomputation for all of the routines below.

VectorHeatSolver::VectorHeatSolver(IntrinsicGeometryInterface& geom, double tCoef=1.0)

Create a new solver for the Vector Heat Method. Precomputation is performed lazily as needed.

  • geom is the geometry (and hence mesh) on which to compute. Note that nearly any geometry object (VertexPositionGeometry, etc) can be passed here.

  • tCoef is the time to use for short time heat flow, as a factor m * h^2, where h is the mean edge length. The default value of 1.0 is almost always sufficient.

Algorithm options (like tCoef) cannot be changed after construction; create a new solver object with the new settings.

Scalar Extension

Given scalar data defined at isolated source locations on a surface, extend it to the entire domain. Each point on the domain will take the value of the nearest source point. Note that the fast diffusion algorithm means the result is a slightly smoothed-out field.

bean scalar extension

Example: 

// your mesh and geometry
VertexPositionGeometry geometry;
SurfaceMesh mesh;

// construct a solver
VectorHeatMethodSolver vhmSolver(geometry);

// some interesting source values
std::vector<std::tuple<Vertex, double>> points;
for (/* ... some inputs ... */ ) {
  Vertex sourceVert = /* something */;
  double sourceVal = /* something */;
  points.emplace_back(sourceVert, sourceVal);
}

// solve!
VertexData<double> scalarExtension = vhmSolver->extendScalar(points);

VertexData<double> VectorHeatSolver::extendScalar(const std::vector<std::tuple<Vertex, double>>& sources)

Compute the nearest-neighbor extension of scalar data defined at isolated vertices to the entire domain. The input is a list of vertices and their corresponding values.

VertexData<double> VectorHeatSolver::extendScalar(const std::vector<std::tuple<SurfacePoint, double>>& sources)

Compute the nearest-neighbor extension of scalar data defined at isolated points to the entire domain. The input is a list of surface points and their corresponding values.

Vector Extension

bean vector extension

Given tangent vectors defined at one or more isolated source locations on a surface, extend transport the vectors across the entire domain according to parallel transport. Each point on the domain will take the value of the nearest source point. Note that the fast diffusion algorithm means the result is a slightly smoothed-out field.

VertexData<Vector2> VectorHeatSolver::transportTangentVectors(Vertex sourceVert, Vector2 sourceVec)

Compute the parallel transport of a vector defined at a single vertex to the entire domain. The input is defined in the tangent space of the source vertex.

VertexData<Vector2> VectorHeatSolver::transportTangentVectors( const std::vector<std::tuple<Vertex, Vector2>>& sources)

Compute the parallel transport of vectors defined at a collection of vertices to the entire domain. The input is defined in the tangent space of each the source vertex.

VertexData<Vector2> VectorHeatSolver::transportTangentVectors( const std::vector<std::tuple<SurfacePoint, Vector2>>& sources)

Compute the parallel transport of vectors defined at a collection of surface points to the entire domain. The input is defined in the tangent space of each the vertex, face, or edge respectively.

Logarithmic Map

The logarithmic map is a very special 2D local parameterization of a surface about a point, where for each point on the surface the magnitude of the log map gives the geodesic distance from the source, and the polar coordinate of the log map gives the direction at which a geodesic must leave the source to arrive at the point.

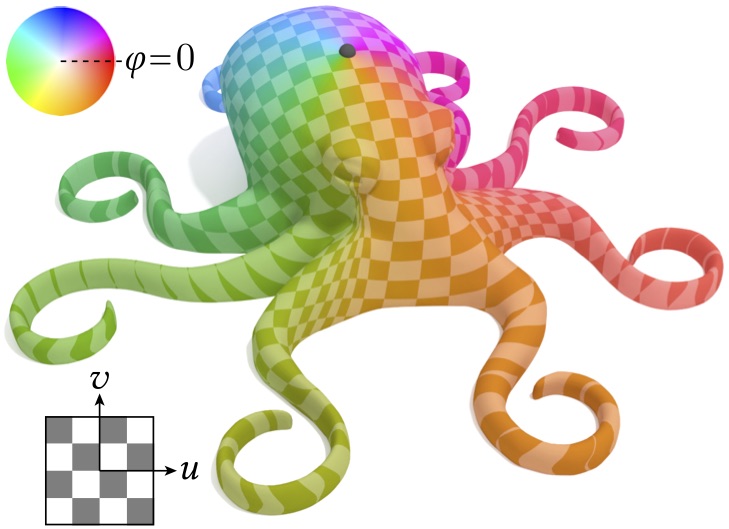
octopus logmap

These routines compute the logarithmic map using the vector heat method or the affine heat method. Several strategies are available, specified by the LogMapStrategy enum:

  • LogMapStrategy::VectorHeat: the original algorithm from “The Vector Heat Method”. Fast, but may have some distortion and warping.
  • LogMapStrategy::AffineLocal: the fast local algorithm from “The Affine Heat Method”. Fast & highly accurate near source. Generates extremely regular coordinates, but may have artifacts if you do not use an intrinsic Delaunay triangulation (see below).
  • LogMapStrategy::AffineAdaptive: the global algorithm from “The Affine Heat Method”. Highest quality. Requires factoring a new matrix each time, so it is significantly slower for repeated solves, though roughly similar cost if just solving once.
VertexData<Vector2> VectorHeatSolver::computeLogMap(const Vertex& sourceVert, LogMapStrategy strategy = LogMapStrategy::VectorHeat)

Compute the logarithmic map with respect to the given source vertex.

The angular coordinate of the log map will be respect to the tangent space of the source vertex.

VertexData<Vector2> VectorHeatSolver::computeLogMap(const SurfacePoint& sourceP, LogMapStrategy strategy = LogMapStrategy::VectorHeat)

Compute the logarithmic map with respect to the given source point, which is a general surface point.

The angular coordinate of the log map will be respect to the tangent space of the source vertex, edge, or face.

intrinsic triangulations make logmaps much more accurate

Using an intrinsic triangulation will make your logarithmic maps dramatically more accurate, especially on meshes with irregular triangles, at little cost. The AffineLocal strategy in particular benefits greatly from operating on a Delaunay intrinsic triangulation.

Example: log maps with intrinsic triangulations 

#include <#include "geometrycentral/surface/signpost_intrinsic_triangulation.h">

// Construct an intrinsic triangulation
SignpostIntrinsicTriangulation signpostTri(*mesh, *geometry);
signpostTri.flipToDelaunay(); // this is the important step, makes it numerically nice!

// Remap the vertex to the intrinsic triangulation, if using
Vertex origSourceVert = /* your vertex */;
Vertex intrinsicSourceVert = signpostTri->equivalentPointOnIntrinsic(SurfacePoint(origSourceVert)).vertex;

// Run the algorithm
VectorHeatMethodSolver solver(signpostTri);
VertexData<Vector2> logmapIntrinsic = solver->computeLogMap(sourceVert, logMapStrategy);

// Copy the logmap back to your original mesh
VertexData<Vector2> logmap = signpostTri->restrictToInput(logmapIntrinsic);

By default, the resulting logarithmic map has coordinates defined in the tangent space of the source point on the intrinsic mesh. At vertices these spaces are the same, but at a general SurfacePoint inside some face you might want to align tangent spaces; see the intrinsic triangulation documentation for details. There may or may not be a builtin method to do the alignment, depending on your setting.

Citation

If these algorithms contribute to academic work, please cite the following paper(s):

@article{sharp2019vector,
  title={The Vector Heat Method},
  author={Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
  journal={ACM Transactions on Graphics (TOG)},
  volume={38},
  number={3},
  pages={24},
  year={2019},
  publisher={ACM}
}

@article{soliman2025affine,
  title={The Affine Heat Method},
  author={Yousuf Soliman, Nicholas Sharp,
  booktitle={Computer Graphics Forum},
  volume={44},
  number={5},
  year={2025}
}